Sometimes, Placement is Everything
Some of the most common questions I’m asked when teaching the Smaart measurement software classes for Rational Acoustics concern microphone placement. Among these are: “Where do I put my mic to get a useful measurement,” “does the position/aim of the mic matter,” and “how many measurement positions do I need?” When you think about it, it’s an interesting proposition to assume we can make a useful measurement of complex electro-acoustical systems loaded into a performance space having a volume in the thousands of cubic meters and have the result somehow summed up at tiny microphone capsule points in space.
Annoyingly enough, the answers to these questions are… more questions. What are we trying to determine? What decisions are we trying to make? In the course of installing, aligning and tuning sound reinforcement rigs, system engineers must make many decisions. Among these are verifying a multitude of performance parameters (make sure our stuff is working), manage the interaction between our individual sub-systems and their environment (make sure it all works together and provides consistent coverage) — and ultimately — adjust and set the system’s response as a whole to fit its intended use (make sure it sounds good).
System alignment requires handling a multitude of issues and dealing with numerous adjustments, and analyzers like Smaart, SIM, Systune, WaveCapture, etc., are powerful tools for helping us make the right decisions.
Measuring the response of our loudspeaker systems requires the use of microphones and therefore, necessarily a decision about where to place these in the acoustic space. When teaching system alignment, I employ the mnemonic “ReLePT” to remember our system alignment checklist — the list of decisions/verifications we must make for each sub-system in our sound system. We are responsible for verifying and adjusting every system’s Response (frequency response and aim/coverage), Level, Polarity and Timing.
Many of the decisions required during the process —particularly for the last three (Level, Polarity and Timing) — are made to manage the interactions between our systems, and are therefore set for one system based on the response of another. In such cases, microphone placements are often driven by determining the point/area of maximum interaction between systems, such as crossovers and overlap zones.
For the purposes of this article, I am limiting its scope to questions about the first element of ReLePT — Response. This is the most common use of our analyzers in system alignment, particularly for simple systems — used to help verify and adjust the frequency response of your speakers.
Our Environment, the Microphones and Tolerances
Clearly, we are not working in a highly controlled laboratory environment, and it’s inappropriate to apply incredibly tight tolerances to our measurements and resulting decisions we are making. To illustrate this point, Fig. 1 shows six frequency response (magnitude) measurements made of a single speaker in a small (approximately 5,500 m3) 200-seat theater from mic positions 20 feet away, in the center of the orchestra seating. All six measurements were made within a one-foot radius of the first measurement. This data set effectively shows the variance in system response due to acoustical differences in reverb structure over that relatively small area of space (approximately the size of a beach ball).
For our measurements, we use flat (frequency-response) omni-directional microphones. These provide us with an excellent, neutral acoustical probe in space. While the spatial variance seen in Figure 1 may or may not be surprising to you, we should be clear that this is not due to an issue of measurement instability, non-repeatability or even microphone variance.
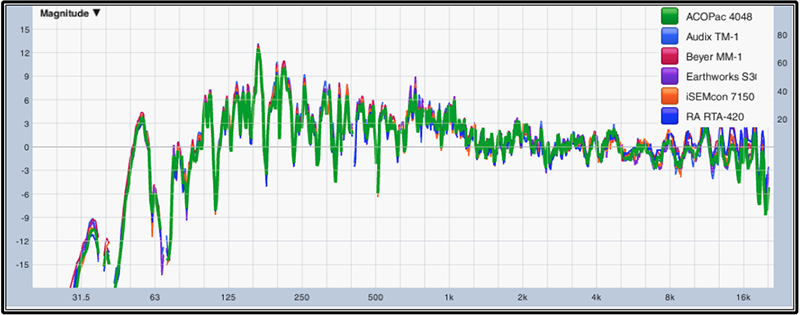To address these questions of consistency and repeatability, consider Fig. 2, which uses six different models/brands of flat, omnidirectional mics to make the same measurement as in Fig. 1. As all of the measurements in Fig. 2 were made at the same point in space (within a ping-pong ball sized area), it is a good illustration of the repeatability of the measurement. And using six different brands/models of flat, omni mics, we also get a good view of the response variance (or lack thereof) between mics.
Given how we are using our microphones and the types of measurements we are making, the response differences between these various mics end up being far less than the spatial variance in our environments. Certainly, there are performance differences between these mics. When considering issues such as max/min SPL, manufacture build quality, self-noise, consistency in sensitivity, audible quality for recording and so on, there may be significant differences between these mics. Fig. 2 points out that when considering the difference in mic performance for how we typically use them for system measurements, besides overall sensitivity (which we adjusted for at the mic preamp), these mics are functionally interchangeable. (BTW — no mic correction files were used in these measurements.)
The Omni Question
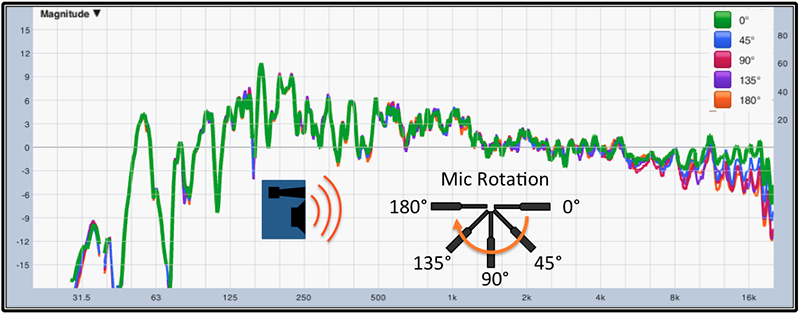A frequent question I get in class is, “Does the direction the an omnidirectional mic is pointing effect the measurement?” The answer to that question is, “Yes, but the real question should be ‘how much’?” Fig. 3 shows a series of five response measurements made with the mic rotated in 45° steps (keeping the capsule in the same place). This clearly illustrates that the mics we use are functionally omnidirectional throughout most of the audible 20 Hz to 20 kHz range. The exception here comes with the on-axis response at the very highest frequencies — generally above 5kHz. Here, the capsule size becomes significant compared to the wavelengths, and we get a build-up of energy whose incidence is on axis to the front of the mic. Omnidirectional mics with the “free-field” designation have HF correction for this on-axis build-up, and therefore roll-off slightly past 90 degrees.
While I know the impact of the mic’s aiming angle is mostly a non-issue, I also know as an engineer making measurements, consistency of method is my friend. So, when I place my mics, I use reasonably matched mics of the same model and point them at the sound source — simply as a way of reducing variables where I can.
Mic Placement — The Near-Field
Let’s start with the near-field. This is one of the most informative mic positions we use in our work. It is the measurement that best isolates the response of the loudspeaker from interactions with its environment, and is our go-to measurement for basic QC — confirmation of proper speaker operation. The primary factor that causes the response variance we saw in Fig. 1 was the influence of the room’s reflected and reverberant energy. In a near-field measurement (approximately 1 to 2 meters on-axis), the influence of that energy is greatly diminished. The closer our speaker is located to boundaries (floor and walls), the greater the influence of the reflected energy.
Fig. 4 shows a comparison of the measured anechoic response (pink trace) vs. two different near-field measurements made at 1m on-axis.
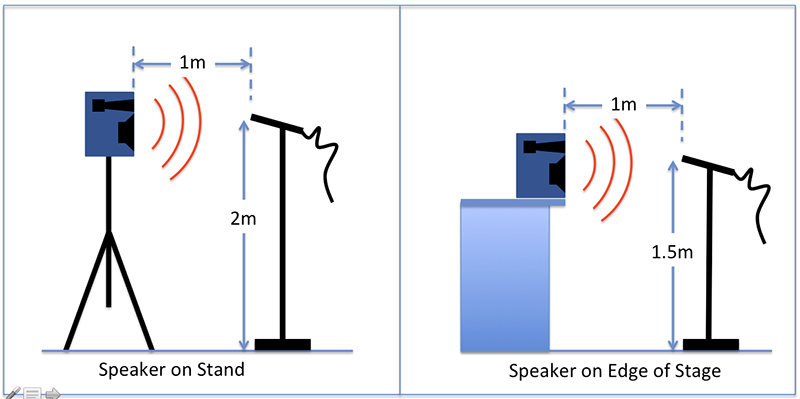Fig. 5 shows two near-field measurements, with the speaker on stand and stage. The first near-field measurement (orange trace) was made with the speaker on a stand with the high driver about 2m from the floor and provided the closer match to anechoic conditions. The second near-field measurement (blue trace) was made with the speaker sitting on the edge of a stage (with a solid front) with the high driver at approximately 1.5m. Both of the near-field measurements match the anechoic measurement closely above 1 kHz (in the high-driver’s range), and both show some ripple from interaction with reflected energy in the low-mid range, with the “speaker on stage” obviously showing more issues.
The important factor here with our two near-field measurements is that they are extremely repeatable and easy to set up in the field. If I am checking or setting a mid- to high-crossover, I am functionally getting the same information I would get in an anechoic chamber. If I am verifying a group of speakers of the same model at a job site prior to installation (as long as I can reproduce the same boundary conditions and mic position), I can very quickly determine if I have issues with inconsistency.
The point here is, when we are working in the field, an extremely common question we ask is, “Is it the response caused by the speaker or room interraction?” Our simple near-field position is our go-to measurement for sorting this out.
Meanwhile, Out in the Room . . .
So now let’s move back into the room, you know, where people will be actually listening to the system. Here, after verifying proper speaker operation and coverage (skip these steps at your peril!), we start to tackle the task of tuning. While in a perfect world of massless inextensible ropes and frictionless planes, using a nice-sounding loudspeaker with a well-behaved response in the near-field/anechoic room would be all we need. Unfortunately, as we get into the listening environment of real-world venues, we need to grapple with the impact of the reverberant energy in the space, and the interaction and sharing of energy between multiple systems. Here, the two most pronounced effects of these interactions are a shift in tonality and possibly degraded intelligibilty.
TIP: Dealing with Excessive Reverberation
The proper/best way to deal with problems caused by reverberant energy is by modifying our room acoustics (often not a practical option) and through our sound system design (the variable most often in our control) to increase our direct-to-reverberant ratio and control how to excite the room. Equalization, while readily available and fun to apply, is the wrong/least effective tool for the job here.
While it would be nice to ask our listening audience to ignore the impact of the reverberant energy and focus only on the direct sound reaching them from our speaker system, that, unfortunately, is not reality. The job for our analysis tool is to help us quantify the impact of this reverberant energy on tonality and intellegibility, and possibly guide us towards making some useful decisions.
For the sake of limiting the scope of this article, I am going to focus on measurements and mic positions in examining the tonality changes caused by a speaker’s interaction with its environment.
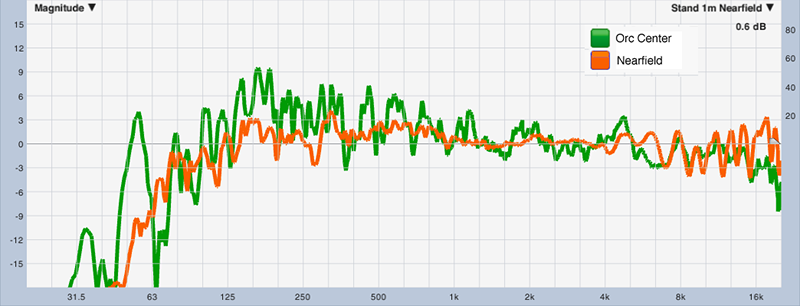As soon as we move our microphone away from the near-field and out into the room, we start to see the impact of the reverberant energy on our response. Fig. 6 shows a comparison of our near-field measurement to a microphone placed 7m (25 feet) away from the speaker in the center of our orchestra level seating.
Note: For all the “Orc” (Orchestra Level seating area) measurements that follow, our microphone used a simple 5-foot “straight stick” mic stand placed in the seating area (soft/padded theatre seats). Also, all measurements were taken within 20° of the center axis in the coverage area of this nominal 110° x 60° (HxV) speaker — basically, in the meat of its coverage.
When normalized for their level differences, we can see the orchestra center measurement has a general build-up of low and mid energy (presumably due to reverberant LF energy) and a slight roll-off of HF energy (possibly due to air absorption). It is also obvious that the “Orc Center” trace shows significantly more response ripple in the same LF region as the build-up due to the interaction of the direct and reverberant energies.
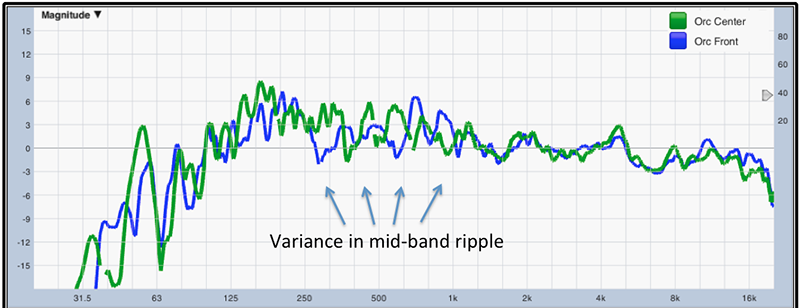As we saw in Fig.1, we should expect that there will be some (and possibly significant) variances in response measurements made within our coverage area. Fig. 7 shows a second measurement — “Orc Front” (blue trace) — that was made by moving our microphone three seating rows (about 10 feet) forward of our “Orc Center” position (indicated in the green trace). Here, in a nutshell, is the cause of the over-equalization nightmares visited upon unsuspecting sound systems by well-meaning system engineers wielding analyzers and an overabundance of DSP/EQ filters.
Imagine, if you will, an engineer who starts with one of the measurements above and places narrow EQ filters to go after the peaks they see in the mid-band. How would that EQ setting hold up at the second position? Both positions are equally valid. Both positions must make use of the same EQ settings.
Hopefully, we begin to see that the task in front of us when making measurements intended for setting an EQ is to derive a response curve that describes the consistent, generalized response of a speaker in its coverage area. Obviously we can’t go after the position-variant ripple that is caused by the reverberant energy — but maybe we can address the general tonal impact of the reverberant energy.
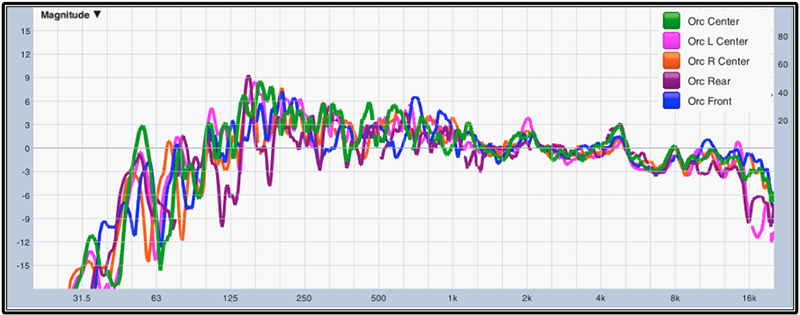With that in mind, Fig. 8 (shows five measurements of our speaker system all made within 3m (10-feet) of our “Orc Center” position. After normalizing our traces for overall level differences between positions, a general response trend becomes pretty obvious. At this point with this data, one would feel pretty confident placing our EQ filters — ones that would generally help out over the majority of the listening area — and we would be hard-pressed to justify a mid-band EQ setting made up of many narrow, ripple-hunting filters.
Taking this multi-position measurement approach a step further, we can mathematically average our individual traces to provide a composite, spatial “average” response. Fig. 9 shows our “Orc Average” trace (black) overlaid on the five response measurements seen in Fig. 8 from which the trace average was created. Notice the relative absence of the mid-band ripple that was present in the individual measurements.
The intent of the average was to find what was consistent between our many positions, and decrease the influence of position-dependent anomalies. In the end, whether you achieve this by visually averaging your data (“eyeball averaging”) or through a mathematical one, the intent is still just not to get caught up in the ripple of a single position. So, if you are going to use only a single position, the question now becomes, can you teach yourself to look for the trends and ignore the ripple? Can you look at the green “Orc Center” measurement we saw in Fig. 6, but see the trends we saw in Figs 8 and 9?
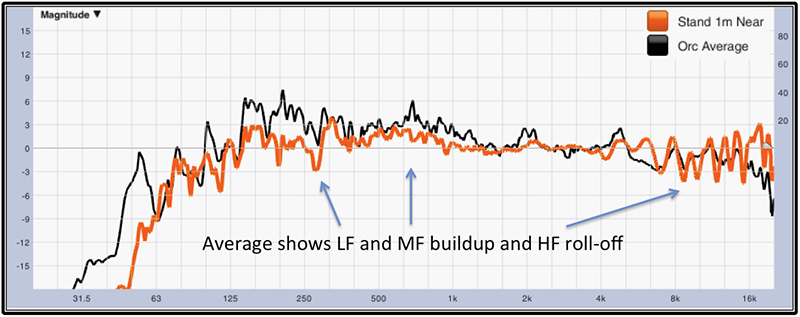Fig. 10 shows our calculated “Orc Average” vs. our near-field measurement. As we are engaged in the process of setting an EQ for our loudspeaker for its listening environment, these measurements now provide an idea of the basic tonal impact of the listening environment on our system. Are we going to address the low and mid frequency buildups, or boost the VHF to get back to flat? In the end, that decision rests with you.
A few interesting questions and answers about our mic positions for our average emerge. First, “how many mic positions we need for a good average?” In practice, I have found three or four positions will suffice (assuming they are all valid positions). Past that, one sees diminishing returns and becomes impractical for implementation when time is an issue.
Second, “Okay, what do you mean by ‘valid positions?’” What we are trying to obtain from our measurements is an idea of the general response of our speaker system in its primary coverage area. The mic positions we use want to be located in the heart of its consistent coverage area — basically near on-axis (within about 15° to 20°) and center of coverage. We are just trying to get enough samples to not be overly influenced by the position-dependent ripple.
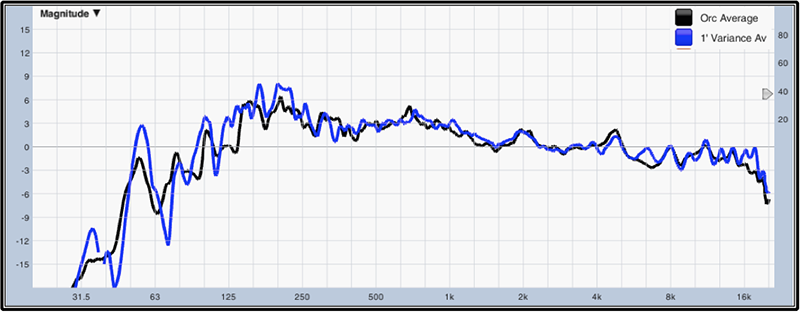This brings up a third question. “How far apart do the mic positions need to be to provide the diversity we need?” Interestingly enough, it’s probably not as far as one would think. Fig. 11 shows the averages of two different sets of measurements. The black trace, “Orc Average” used our “orc center” position and four measurement positions placed within 10 feet forward, behind, left and right. The blue trace, “1-foot Variance Avg” started with our same “orc center” position, but used four measurement positions that were all within only a 1-foot radius.
The biggest difference between the results of the two averages in Fig. 11 can be seen in the LF ripple. The larger radius for positions provided us with less ripple and marginally better data to make LF decisions on. In practice, a 5- to 10-foot radius for our positions should be fine.
Actionable Data
We use our measurement systems to help answer the questions we encounter as we verify and align our systems. In the end, we choose our mic positions based on the questions we are trying to answer — I know that sounds obvious. The biggest problems I have seen with users taking measurements and making decisions based on them generally root back to a lack of understanding or acknowledgement of the degree of variance in our environment. But armed with an understanding of the basics, you will be better equipped to deal with a challenging acoustical environment.
In a future issue, we’ll continue the discussion, taking a look at measuring in empty rooms and also examining ground-plane measurements.
Jamie Anderson has spent nearly two decades teaching sound system engineering, measurement and alignment for SIA, EAW, Meyer Sound (SIM) and Rational Acoustics’ Smaart and was one of the co-founders of that company in 2008.
