Horns of various sizes and shapes have been with us since the formative days of professional sound reinforcement. Whether stacked on top of a bass bin in the early days, or carefully integrated into the injection molded housing of a powered loudspeaker today, horns are here to stay.
Early horns were primarily concerned with optimum acoustic loading of the compression driver. As compression driver performance has improved, directional control has superseded acoustic “loading” as the most critical function performed by loudspeaker horns. This month, we’ll provide a crash course in horn function, the rise of controlled directivity and glimpse into the advanced techniques used in modern horn design.
From Pressure to (Volume) Velocity
All horn and waveguides perform one specific task, namely the transition of sound from one end of a tube with a given cross-sectional area to the other end of that tube with a different cross-sectional area. More specifically, horns are designed in such a way that a high pressure near the sound source (e.g., compression driver) is converted to a high volume velocity near the horn’s exit, also known as the horn “mouth.”
Pressure, which is defined as force/area, is a concept many are familiar with. Not so with volume velocity. Volume velocity is defined as particle velocity * area. It can be thought of as the amount of air particles that are being swept back and forth at a given speed in a given direction as the sound wave passes by. It is important to note that this particle velocity is not the speed of sound, but rather the speed of the displacement of the air particles from their rest position as the sound wave moves past. The particle velocity is typically much lower than the speed of sound, and there is no net displacement of the air particles.
A device like a compression driver is able to exert a high force, and therefore a high pressure, on a comparatively small area of air molecules. One would like to distribute that pressurization over a larger region of air molecules moving in concert with each other at a higher particle velocity. A horn’s expanding length accomplishes this transition in a controlled fashion, and this transformation drove the original development of loudspeaker horns.
Moving Through the Horn
Moving away from the compression driver, the sound wave travels in an arc through the expanding portion of the horn, known as the flare, towards the mouth. While the flare is expanding, some fraction of the air particle’s movement is directly out of the horn, and some is in the direction of the flare expansion. Air particles at the flare wall must move along the wall, as the physical boundary prevents them from expanding further outward. The wave front that moves through the horn is defined as perpendicular (i.e., at right angles) to the direction of propagation. The speed of sound is constant, so the distance traveled by the sound wave in any given amount of time is also constant. However, because the horn is expanding, the distance along the horn wall is farther than the same path down the center of the horn. This means that the wavefront becomes progressively more rounded as it moves through the flare.
As sound travels through the horn, a portion of the energy from the sound wave does not emerge from the mouth, but is instead returned back down towards the throat. This effect is most pronounced at the abrupt flare termination of the horn mouth. To understand this behavior in a more intuitive sense, it is useful to consider an analogous circumstance from the world of optics.
When you stand in front a pane glass window, you can see through the window, but you can also see a faint a reflection of yourself back in the glass. The backwards reflection in the glass derives from the fact that glass and air do not have the same index of refraction. When light transitions between different physical mediums (e.g., glass and air), the mismatch in index of refraction causes the reflection.
In acoustics, there is a quantity analogous to index of refraction known as the acoustic impedance. The acoustic impedance is defined as pressure/volume velocity. We’ve already established that the relationship between pressure and volume velocity changes as sound moves through the horn. Another way of saying this is that the acoustic impedance is changing through the horn. This change in acoustic impedance is most drastic at the horn mouth, where the horn’s controlled expansion stops and free space begins. This sharp change results in the most pronounced reflection back into the horn. This reflected energy then travels back through the horn and re-emerges later in time. Because real horns are not infinitely long, and therefore always have a mouth, reflections at the end of the horn are something horn designers must consider.
The Rise of Directional Control
For modern professional loudspeaker horns, directional control is arguably the most important behavior and feature. From small ceiling loudspeakers to line array waveguides in large concert systems, loudspeaker designers are looking to influence where sound travels in space. The core idea of directional control, or directivity, is that we can change the loudness of sound based on the direction it travels relative to the horn flare’s physical location. Generally, the desired nature of this behavior is that angles in front of the horn will receive broadband sound of high loudness, while those off to the sides and back of the horn will experience greatly reduced sound levels.
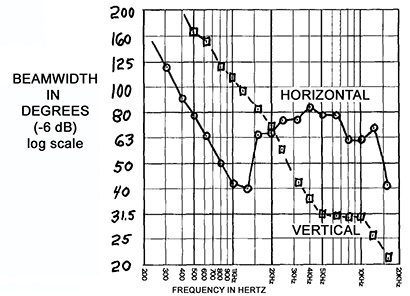There have been a number of approaches towards directional control, with varying degrees of success. For example, one of the early attempts at directional control is the radial horn (see Fig. 1). The classic radial horn was a dual-profile horn flare. The flare profile was typically conical in one plane, and typically exponential in the other plane. The idea was that the straight walls of the conical flare would provide directional control, while the exponential flare in the other plane helped provide good acoustic loading for the compression driver. As shown in Fig. 2, the directional response in the conical plane was somewhat even, but the coverage angle still narrowed rapidly in the other plane. Even this moderate degree of directional control was a substantial improvement over horn designs that had been used previously.
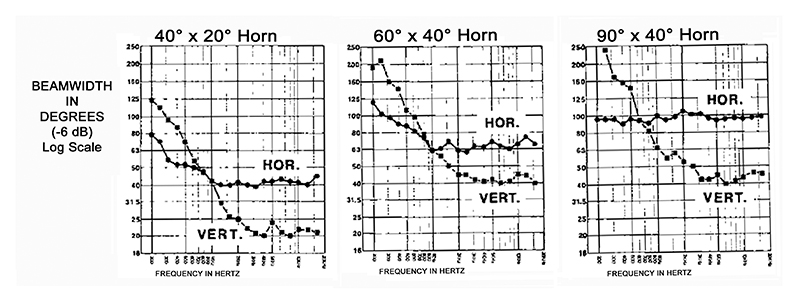
Seeking to reduce these compromises, in 1975, Don Keele of Electro-Voice published a seminal AES paper entitled “What’s so Sacred About Exponential Horns?” In this paper he enumerates what is now broadly known as the Constant Directivity, or CD, horn (Fig. 3). Keele demonstrated the general effectiveness of this horn configuration with directional plots for multiple different coverage angles (Fig. 4).
The Constant Directivity horn flare had three distinctive regions, each with a specific purpose. Adjacent to the compression driver, was an exponential flare designed to provide acoustic loading. Moving outwards from the exponential throat section is a section with conical flare (i.e., straight side walls). This section provides the Constant Directivity characteristic of the horn’s angular coverage. A third region near the horn mouth is a secondary expansion designed to reduce reflections, and narrowing of coverage caused by the abrupt termination of the horn mouth.
At the core of the Constant Directivity horn’s behavior is the conical flare section with straight side walls. This section of the flare sets the coverage angle by providing a constant direction of propagation for the sound wave at the horn wall, due to the wall being straight. The majority of the frequency spectrum leaves the horn flare and travels into free space in the conical area of the horn, where the exit angle is constant. The throat’s build-up to the conical section and the secondary flare at the mouth then serve the purpose of minimizing secondary horn behaviors from polluting Constant Directivity. In other words, carefully shaping the throat and mouth allows the middle of the horn to properly perform its task of consistent directionality.
Ever since Keele’s introduction of the Constant Directivity horn, manufacturers from all corners of the globe have continued to pursue improvements in the evenness of loudspeaker coverage. As professional loudspeakers will likely always need to place sound on the audience, the goal of controlled, consistent directivity will be with us forevermore.
Modern Solutions
There was an era where loudspeaker directional coverage in challenging environments was dominated by large compression drivers on very large constant directivity horns. That “flying junkyard” era has largely passed for the industry, and now the focus is modularizing the loudspeaker components, and their directivity control, into the most flexible and scalable packages feasible.
As a result of the push to more modular solutions, modern loudspeaker arrays tend to rely on more than just loudspeaker horns for directivity control, but rather commonly operate in a hybrid configuration where directional control at the higher frequencies comes from a horn waveguide, and directional control of mid and lower frequencies derives from the controlled spacing and signal fed the other transducers. Essentially all vertical arrays on the market operate in this manner.
Even the fully horn-loaded line array products that exist behave in a manner not unlike the old multi-cellular horns in the midrange and lower frequencies. At these frequencies the directivity is shaped by the collective output of a number of horn cells formed by each box in the line array.
Computers are now shaping the way these modern, modular loudspeakers are modeled, designed and processed. A brief overview of the history of horn analysis helps frame the improvements from computers. Early in the 20th century it became interesting to try to put mathematical description to sound moving through an expanding horn flare. The first systematic math for this is known as Webster’s horn equation, developed in 1919 by Arthur Webster.
Webster’s equation makes a key assumption that the shape of a pressure wave in a horn flare can be described by a single parameter wave shape. There are three single parameter description of a wave’s shape: the traveling plane, the expanding cylinder, and the expanding sphere. Waves moving in real-world horns generally don’t travel in any of these shapes. However, much of the existing mathematical work for horns treats the waves moving as a plane wave to simplify the calculations. Thus, while Webster helped people tackle the math of horns in the pre-computer era, there is a glaring assumption built into the equation. At the time Keele developed the Constant Directivity approach, horn designers were still doing calculations on models built around the plane wave assumption.
Computers now allow working with the fundamental wave propagation math that is behind sound waves moving in a horn. This math is formulated in special way using an equation called the Helmholtz integral. The Helmholtz integral is then directly solved by computers using a numerical process known as the Boundary Element Method (BEM). Fig. 5 shows the schematic of a horn analyzed via BEM. The triangles on the surface of the horn represent the mesh of points where the equations are analyzed. Working with BEM requires no specific assumptions about the shape of the wave as it travels through the horn. BEM allows designers to develop horn flares with consistent directivity characteristics that have more subtle transition from throat to mouth. BEM calculations can also be performed for waves in other environments, such as compression driver phase plugs, loudspeaker enclosures, arrays of loudspeakers, etc.
Better modeling and measurement of loudspeaker horns allows for smarter compromises in sound system development. Horns are inherently reflective devices, and the question of reducing horn reflections remains a relevant one today, as the industry tries to improve the sound emerging from horns that are placed in increasingly compact loudspeakers. Smaller horn mouths can lead to more problematic reflections back down the horn. The same limitations holds true at the transition between line array wave-shaping devices and the horns that they exit into.
Many wave-shaping devices for vertical arrays make assumptions about the shape of the incoming sound from the compression driver. Application of advanced computer modeling to the compression driver insures that the wave that leaves the compression behaves as desired, especially at very high frequencies where the geometry inside the compression driver can adversely shape the output wave. This helps insure the waves entering the horn from the compression driver match the assumptions the horn was designed on.
Conclusion
Improvements notwithstanding, certain quirks of horns will likely never be eliminated. Horns will remain devices that experience some reflections, and devices whose ultimate performance depends on the wavelength of sound that travels through them. We will probably always desire them to be smaller, but physics will continue to dictate their size to provide broadband pattern control.
It is apparent that much has improved in our ability to model, measure, and process the sonic character of the horns we rely on to direct sound coverage over the audience. Computing power allows us to grasp hold of something as fleeting as a sound wave leaving the compression driver for a short flight through the horn out into the open air. Computers allow us to visualize something our physical senses otherwise miss completely. We look forward to seeing what other clever bits of performance designers will continue to squeeze out of the complexities inherent in horns as more of the industry adopts advanced approaches to horn design.
