With the apparent ease of predicting vented loudspeaker response, it is tempting to blindly follow the software and assume that the curve on the screen is representative of what the loudspeaker will produce at any volume level. But the reality of loudspeaker performance is more complicated than is indicated from some piece of software found on the Internet.
The Thiele-Small (T-S) parameters now provided on every driver datasheet do not provide insight into how drivers perform when the music is pumping and the drivers are required to produce a lot of output. Loudspeaker drivers are messy devices, producing more distortion than the rest of the audio signal chain combined. The T-S parameters do not capture any of that messy behavior or provide insights into whether one driver will have cleaner performance than another.
This month we introduce three plots that help quantify the performance of drivers under real-world conditions at high SPL’s. The plots are captured by equipment made by a German company called Klippel, GmbH. Transducer designers can use these plots to improve driver design, and loudspeaker enclosure designers can use them to understand how drivers will perform at high volume. But before we show the Klippel plots, a brief overview of what is not captured by the T-S parameters.
Thiele-Small Crash Course
Using the Thiele-Small (T-S) parameters, one can calculate the acoustic response of the driver and enclosure together. Neville Thiele and Richard Small were acoustical researchers that defined parameters that could be measured for real loudspeaker drivers and inserted into mathematical models. This type of analysis is known as a “lumped element” modeling and was used for electrical circuits before being applied to loudspeakers and their enclosures.
Understanding lumped element modeling is fairly straightforward. Each mechanical or electrical behavior of a loudspeaker has an analogous description available in the world of electric circuit components (i.e., resistors, capacitors and inductors). The entire loudspeaker and box can be represented by a collection of electric circuit elements, and the performance analyzed with the same set of tools built to describe the behavior of circuits with many elements. Nearly 50 years ago this was an extremely powerful technique and is still broadly useful today.
One key limitation of the T-S parameters is that they are “small signal” parameters, which means that they accurately capture the performance of the loudspeaker at low output volume. Further, the parameters have fixed values. They do not change for the driver based on different input levels. This is not indicative of the mechanical reality of drivers, where the electromechanical parameters of loudspeakers change during a gig.
For example, loudspeakers are bad at turning electricity into sound and the remaining electrical energy is dissipated as heat. This heat raises the temperature of the driver voice coil and magnet structure. As the voice coil temperature rises, physics dictates that the voice coil wire does not conduct as effectively, and this causes the driver voice coil resistance to increase. The thermal change in the driver results in a shift to multiple T-S parameters. This shift is not quantified by the numbers on the datasheet, which were probably measured at room temperature.
Beyond T-S
Realizing the Thiele-Small parameters are an incomplete picture of loudspeaker driver behavior, what should be done to improve the data about drivers? The thermal performance alluded to above is part of the puzzle, and another component is characterizing how a drivers’ parameters change as it moves in and out to generate sound. The process of the cone moving in and out is called “excursion” and the three plots presented in this article each capture a parameter change based on the position of the cone during excursion. Because the Klippel analyzer can capture driver parameters versus excursion, it provides insight into how the driver performs when the cone is really moving.
Before describing the plots, let me briefly note their origin. The data below are from Italian loudspeaker B&C, and were captured by the Klippel analyzer for one of its 21-inch woofers. The data in all three plots is not simulated, but measured from real drivers. Providing real data for plots that people are not familiar with takes a degree of chutzpah, and B&C’s support fowr this article is much appreciated.
 Figure 1: Bl (X)
Figure 1: Bl (X)
Since a picture is worth many words, we now introduce Bl (X), the first of the three fundamental Klippel plots (Fig. 1). “Bl” is the strength of the driver’s magnetic field times the amount of wire the driver placed in that magnetic field. It is a measure of the strength of force that moves the cone inwards and outwards. On the Bl (X) plot, as well as the other Klippel plots, the “X” represents cone excursion. The larger the value of X, the greater the cone’s distance from its nominal center resting place. The Bl (X) curve therefore shows how strong and consistent the force acting on the cone will be at different cone positions.
A transducer engineer wants the central plateau of the Bl (X) curve to be as flat, broad and symmetric as possible. The grey dashed line on the plot represents the idealized, symmetric behavior that a particular driver would want to match. The more broad the flat section of the Bl (X) curve, the greater the driver’s linear excursion capability will be before distortion starts to increase. Further, the driver designer wants the curve to be as symmetric as possible to reduce the amount of even-order harmonic distortion. Finally, the driver designer wants the tails on either side of the plateau to be as similar as possible so that driver overloads in a graceful fashion at very high excursion.
Creating a broad symmetric Bl (X) curve is not a trivial process. The driver’s suspension must hold the cone precisely when at rest, and lots of simulation work must be done to make the magnetic behavior symmetric about the rest position. Since the driver in question here is a woofer designed for low frequency output, the goal is to facilitate as much linear excursion as possible, as evidenced by a broad flat plateau.
Armed with Klippel data for multiple drivers, one can compare the width and symmetry of the plateau region on the Bl (X) curve to determine which driver will have the largest amount of linear excursion from its electrical motor structure. The Bl (X) provides far more information about the excursion behavior than a commonly listed parameter called Xmax. Xmax has no universally agreed upon definition, and thus generally cannot be used to compare drivers on an apples-to-apples basis.
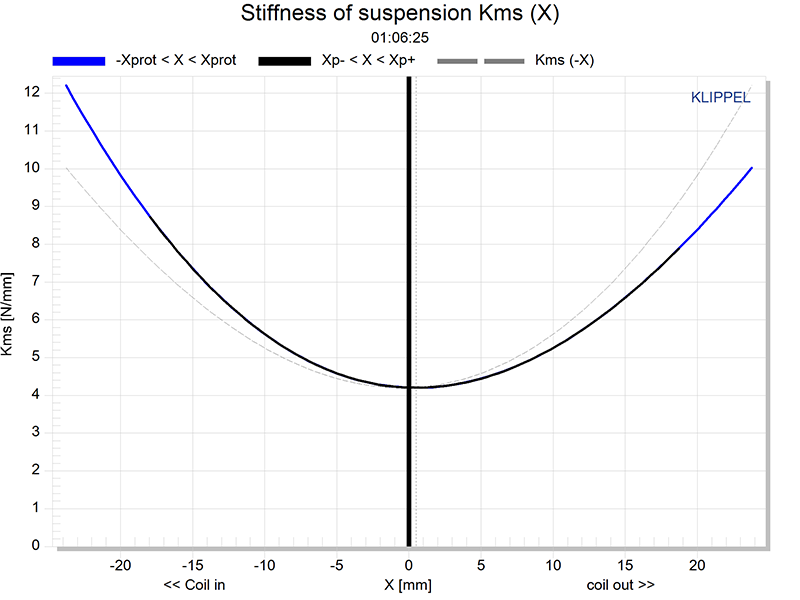
Figure 2: Kms (X)
Kms (X) is the mechanical analog of Bl (X). It characterizes the uniformity of the restoring force applied to the cone by the driver’s mechanical elements like the spider and surround. Driver manufacturers don’t necessarily want the restoring force to be uniform throughout the driver’s excursion. It can be a useful tool to improve the overall combined linearity, mechanical plus electrical, of the driver. Generally the more symmetric the Kms (X) plot, the better the driver’s distortion performance will be due to mechanical considerations. Again, as in the Bl (X) graph, the dashed grey line in Fig. 2 represents the idealized symmetric Kms (X) curve for the driver in question. Suspension materials and configurations that remain symmetric over a wide range of excursions are part of the closely held intellectual property important to a loudspeaker driver manufacturer.
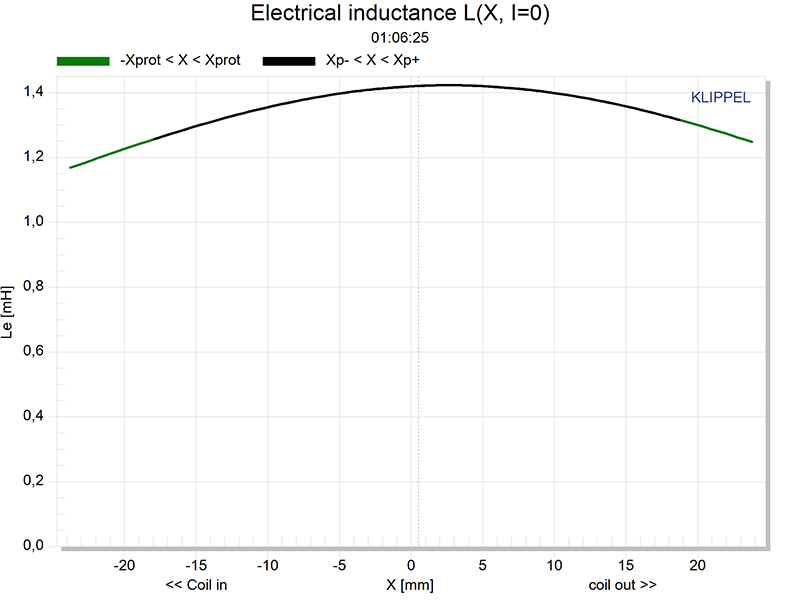
Figure 3: Le (X)
The final plot in our article shows how the driver’s inductance (Le), changes versus excursion “X.” Inductance is a measure of the energy that is stored in the driver’s magnetic field. The Le (X) plot captures information about the combined magnetic fields of the voice coil and the surrounding magnet structure. Any change in the inductance of the driver means that energy is being stored magnetically in a way that is not constant with excursion. The ideal Le (X) curve would be a completely flat line at one value of inductance.
A useful way to think about the Le (X) curve is that it shows us when energy from the amplifier is being stored temporarily by the driver, rather than being put forth to move the cone. While the presence of some of this temporary energy storage is unavoidable, we want that behavior to be as consistent as possible at different positions of the cone. Transducer designers can change the shape of the magnet structure and add devices called “shorting rings” to make the Le (X) curve more flat. These tweaks can result in drivers with lower distortion.
Summation
The greater the amplifier input, the more the limitations of the driver and enclosure will become apparent. The Klippel plots provide a unique insight into when the driver performance will start to exhibit more distortion, and provide a concrete comparison for between drivers at high output levels. Bl (X), Kms (X) and Le (X) are powerful tools to refine transducer design or help the driver selection process.
This sort of insight was completely lacking from the original T-S parameters. One driver might simulate to have smoother low frequency response by the T-S parameters, but in reality have problems with linear excursion and exhibit all kinds of distortion when operated in anger. Of course, the latter behavior would only become evident after the driver was in hand and in an enclosure. Today, thanks to Klippel plots, one can have much more confidence of the gigging performance before any plywood is cut.
Personally, I consider the Klippel plots an integral part of the information about a transducer, and I look forward to the day when data sheets commonly include the Klippel data in the same manner that Thiele-Small parameters became universal. The net result will be better performing loudspeakers, and better shows for the patrons we serve.
Phil Graham is FOH’s regular technical contributor and resident scientist. Email him at: pgraham@fohonline.com.



