
Note: Written by the late, great John Eargle (and re-published courtesy of Harman Professional), this article is excerpted from a book he co-authored with Chris Foreman entitled Audio Engineering for Sound Reinforcement. Eargle, JBL’s VP of engineering for many years, was a well-known author, consultant and recording engineer with more than 250 CD releases; and his cinema work garnered him a Technical Oscar in 2001. His books are industry benchmarks.
(To download a PDF of this FRONT of HOUSE Tech Feature, CLICK HERE)
The behavior of sound indoors is fairly complex, but fortunately a number of simplifying assumptions make the analysis much easier.
The Indoor Sound Field
When a steady sound source is turned on in a room, there is first a short time period during which the sound reaches all parts of the space and establishes a steady-state condition.
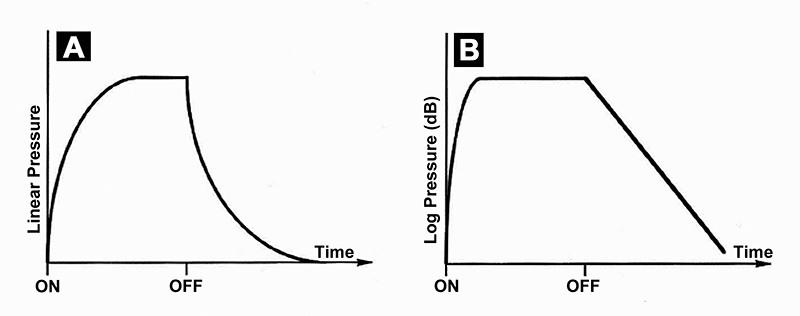
When this condition has been reached, sound power is absorbed at the room boundaries at the same rate at which it is emitted by the source. After the steady-state condition has been reached, let the sound source be turned off. We then observe that sound in the room dies out after some short period of time. Fig. 1-24 shows the nature of the buildup and eventual decay of sound in the room. The curve shown at A describes the variation in sound pressure, while the curve shown at B describes the build-up and decay processes in terms of level. The process shown at B is in fact the way we hear the sound rise and decay, since our hearing is essentially exponential in response.
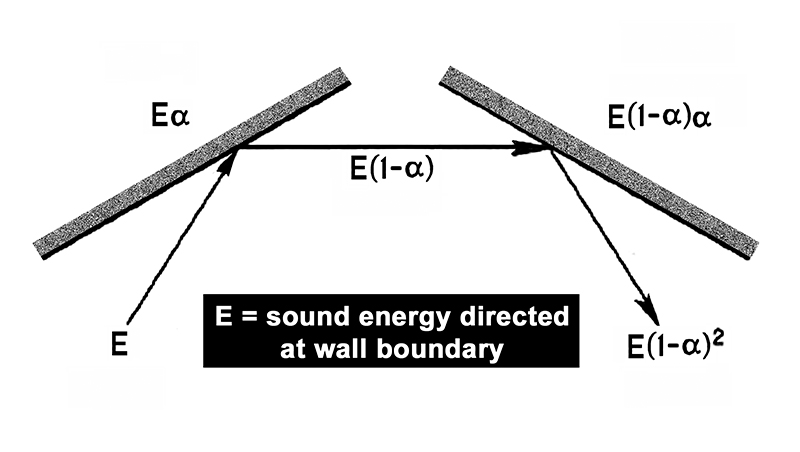
We might think of many individual “rays” of sound, each going its own way from the source in a different direction. Statistically, it can be shown that the average distance (mean free path) a ray of sound travels in the room between successive encounters with boundaries is given by:
Mean free path = 4V/S
where V is the room volume and S is the total area of the room boundaries. (The equation holds with either English or metric units.) This process is shown in Fig. 1-25. While each surface in the room may have its own absorption coefficient “α,” there will effectively be, after several reflections through the room, an average absorption coefficient, which we designate as α.
The Reverberant Field and Reverberation Time
After the sound source has been turned off, we will hear a relatively smooth decay of sound in the room. The length of time it takes for the sound to decay 60 dB after the power source has been turned off is known as the reverberation time and is an important qualifier for music or speech perception in any space. The Sabine Equation (below) gives a fairly accurate estimate of reverberation time in fairly “live” spaces, those in which the average absorption is no greater than about 0.25.
Reverberation Time (TA, in seconds)
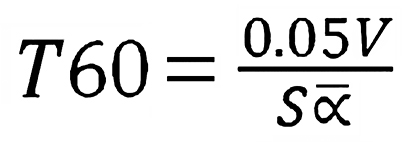
where V is the room volume in cubic feet, S is the room boundary area in square feet, and alpha-bar is the average absorption coefficient in the room.
Similarly, in metric units, the equation is:
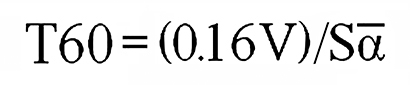
where V is the room volume in cubic meters and S is the room boundary area in square meters. Alpha-bar will be the same in both cases.
We can measure reverberation time today with any number of acoustical data gathering and analysis programs for personal computers. If we have enough data on the room’s physical aspects, we can calculate it by estimating the room volume, surface area, and deriving the average absorption coefficient as follows:
Average Absorption Coefficient
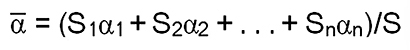
where S1, S2, … Sn represent individual surfaces in the room and α1, α2 … αn represent their respective absorption coefficients. S is the total boundary surface area of the room. The unit of absorption is the sabin and is equivalent to one square foot (or square meter in the SI system) of totally absorptive surface area. There are other equations for reverberation time, but none as useful and simple as the Sabine equation used here.
Direct, Developing and Decaying Sound Fields in a Room
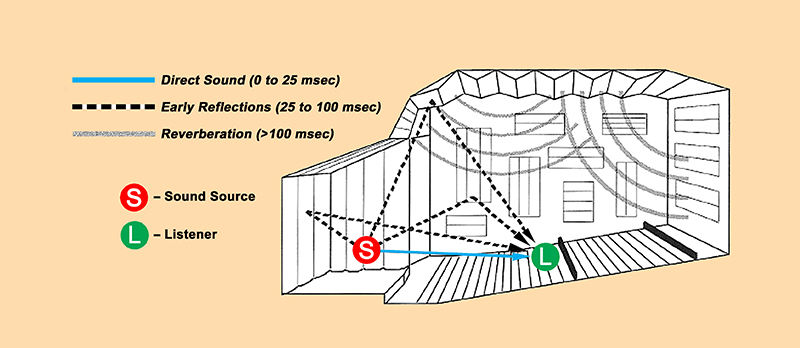
Now, let’s replace the steady source of sound with a short impulse and see how sound develops in the room. In Fig. 1-26 we see what happens during the first 25 milliseconds (msec) or so after an impulse sound takes place on stage. At first, only the direct sound reaches the listener. Then, during the next interval (25 to 100 msec) a volley of discrete, developing reflections reach the listener, most of them arriving from the front and sides of the room. Finally, beyond 100 msec, decaying sound (reverberation) arrives from all directions in the room more or less equally.
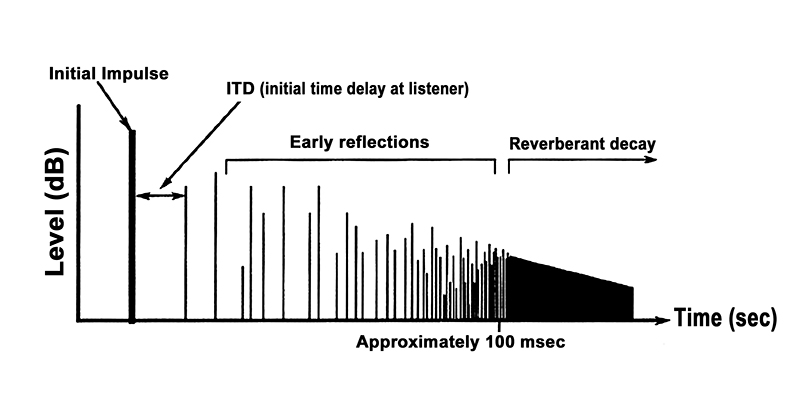
The time response as heard by the listener is shown in Fig. 1-27. Here, we can identify the initial time delay (ITD), that short period of time after the arrival of the direct sound, but before the first reflection arrives. In most moderate size listening spaces this gap is about 25 msec. Acousticians often speak of the early sound field, which exists up to approximately 100 msec after the arrival of direct sound. It is important in that it adds loudness and a sense of spaciousness to music presented in the room. If the early sound field is too loud, as may be the case in small, live rooms, the listener may be bothered by blurring and “smearing” of musical and speech details.
Reverberation, including early and decaying sound, often enhances music but is beneficial for speech only when it is fairly short. One of our main jobs in sound reinforcement design is to minimize the effect of the reverberant field without actually reducing it.
For more info on room acoustics topics, including: Critical Distance, increasing the Direct-to-Reverberant Ratio and Standing Waves, see the second half of Chapter 1 of Audio Engineering for Sound Reinforcement at www.proaudioencyclopedia.com/acoustical-fundamentals; or David Kennedy’s basic introduction to room acoustics at www.line-arrays.com/acoustics.html.
David K. Kennedy, a consultant on architectural acoustics and sound system design, has designed hundreds of sound systems for churches, schools, performing arts centers and AV contractors. Visit him at immersive-pa.com.



