
Note: Written by the late, great John Eargle (and re-published courtesy of Harman Professional), this article is excerpted from a book he co-authored with Chris Foreman entitled Audio Engineering for Sound Reinforcement. Eargle, JBL’s VP of engineering for many years, was a well-known author and consultant, a recording engineer with more than 250 CD releases and his cinema work garnered him a Technical Oscar in 2001. His books are industry benchmarks.
To download a PDF of this Tech Feature, go to https://fohonline.com/site/wp-content/uploads/tech-1.pdf
When we speak only in terms of sound pressure, we are dealing with numbers, which, from the softest audible sounds to the loudest, cover a million-to-one ratio. This would involve some rather large and clumsy numbers, and in the early days of telephone research, mathematicians simplified the notation with the introduction of the bel and the decibel.
How We Measure Sound: The Decibel (dB)
In using decibels, we are expressing the level of one signal with respect to another (the term level is exclusively used in audio engineering for ratios given in dB): bel = 10 log10 (W/W0),
where W0 is a reference power and W is any other power. For example, let our reference power be one watt and let W = 10 watts. Then: Ratio in bels = 10 log (10/1) = 1 bel.
We can state that the level of 10 watts relative to one watt is 1 bel.
For more convenient scaling of the numbers, we more commonly use the decibel, which is defined as: Ratio in dB = 10 log (W/W0)
and in this case, the ratio is: 10 log (10/1) = 10 dB.
From this basic definition, we can construct the following chart, which gives the level in dB for various powers, all referenced to one watt:

Here, the range of power values is a million-to-one; using levels in dB, we have reduced this numerical range to a far more convenient 50-to-one range.
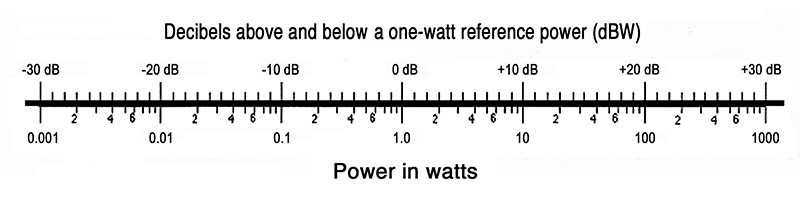
Fig. 1-14 presents a convenient nomograph that lets us read the decibel level directly between any two power values over the range given above.
A given difference in dB always corresponds to a given ratio in power. For instance, a 2-to-1 ratio in power always represents a 3 dB change in level. Look carefully at Fig. 1-14; pick any pair of powers with a 2-to-1 ratio, then carefully read the difference in dB directly adjacent on the scale and you will see that the difference is always 3 dB. For example, locate 40 and 80 on the power (watt) scale; looking at the adjacent levels we read 16 and 19 dB. Thus, 19 – 16 = 3 dB.
Note also that any 10-to-1 power ratio is always represented by a 10 dB difference in level.

Relating the Decibel to Sound Pressure
We do not normally measure sound power; instead, we measure RMS sound pressure using a sound level meter (SLM), which is calibrated directly in dB. You can invest in a precision meter, such as the NTI unit shown in Fig. 1-15, but for many applications an SLM app for your phone may suffice. Acoustical power is proportional to the square of sound pressure; therefore, doubling the sound pressure will produce a quadrupling of acoustical power. As we have seen, doubling power represents a 3 dB level increase; doubling it again will add another 3 dB, making 6 dB. Therefore, we can construct a new scale in which a doubling of sound pressure corresponds to a 6 dB increase in sound pressure level (SPL), and a 10 times increase in sound pressure corresponds to a 20 dB increase in SPL. This new scale is shown in Fig. 1-16. The “zero” dB reference pressure for this scale has been chosen as 20 micropascals, which is the threshold of hearing in the 3k to 4k Hz range for persons with normal hearing.

A Free, Progressive Sound Wave: Inverse Square Law
Consider a small sound source outdoors located away from any reflecting surfaces and emitting a continuous signal. We will measure the sound pressure at some reference distance “d” and detect a pressure value of p1. Now, if we move to a distance that is twice “d,” we will detect a new pressure value, p2, which will be one-half of p1. This process may be carried out indefinitely, with each doubling of distance producing a halving of pressure. The process is shown in Fig. 1-17.
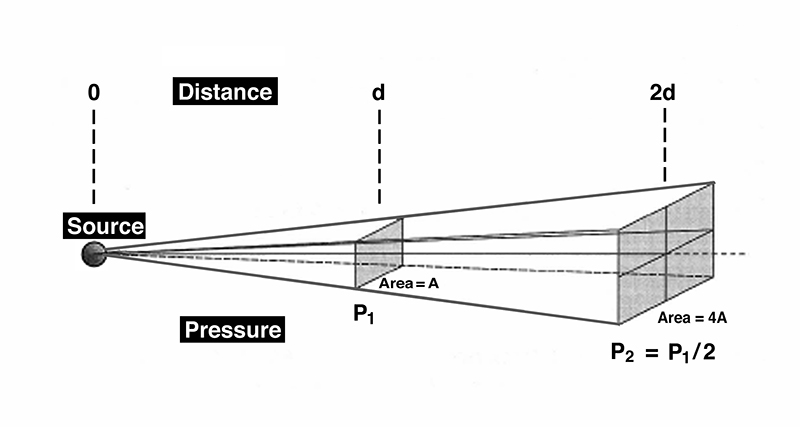
At distance “d” in Fig. 1-17, we show an area through which passes a certain amount of radiated sound power. At a distance of 2d, that same power is now radiated through four-times the original area. The relationship of quadrupling the number of squares for the doubling of distance is referred to as the inverse square law.
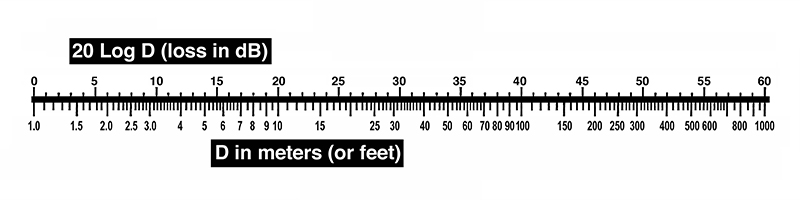
The halving of sound pressure at distance 2d represents a drop in sound pressure level of 6 dB relative to distance “d” and we can now construct a new nomograph for determining sound pressure levels as they vary with distance from a source in a reflection-free environment (so-called free space). The new nomograph is shown in Fig. 1-18. In order to show the correspondence between doubling distance and reducing the level by 6 dB, we must plot 20 log (D/D0), where D0 is our reference distance of one foot (or one meter).
As an example of using this nomograph, let us assume that a given source produces a sound pressure level of 94 dB at a distance of one meter. What will the level be at a distance of 20 meters? Referring to the nomograph, locate the distance 20 on the foot (meter) scale. Directly adjacent to 20 read 26 dB. The level will then be 94 – 26 = 68 dB SPL.
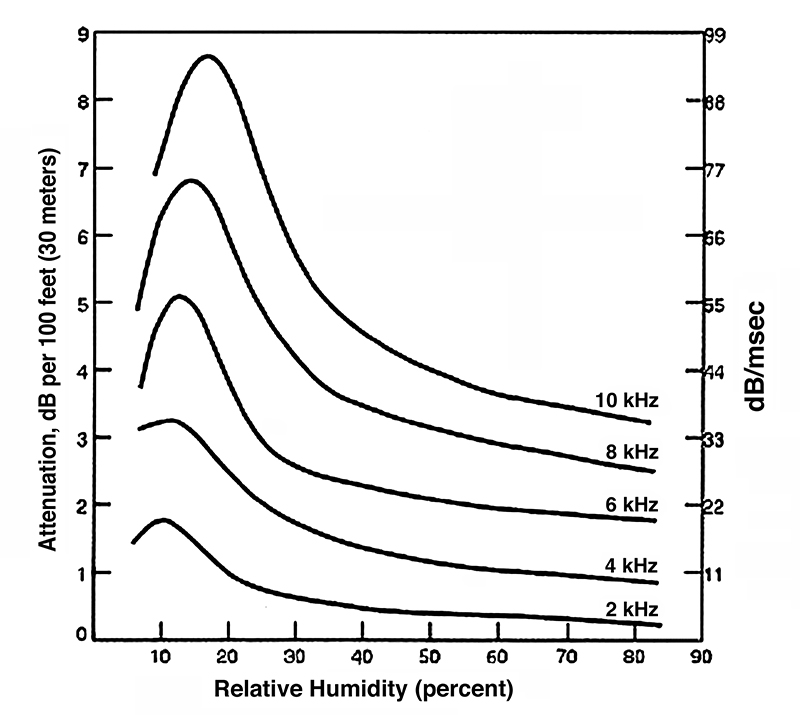
In addition to level losses over distance due to the inverse square effect, there is additional loss at high frequencies due to air absorption. An indication of this is shown in Fig. 1-19. Along the left vertical axis, you will note the excess attenuation in dB per 100 feet (30 meters) encountered over long distances. Note the high dependence on relative humidity; high frequency losses are greatest when relative humidity is in the range of 20% and least when relative humidity is high.
As an example of air losses at high frequencies when relative humidity is 30%, let’s calculate the loss in dB between distances of 2 feet and 200 feet from a source. At low frequencies (below about 500 Hz), only the inverse square loss will be significant. Using the nomograph in Fig. 1-18, we can see that the loss will be 40 dB. For a frequency of 10k Hz, there will be an additional loss due to absorption in the air itself. From Fig. 1-19, we can read the loss per 100 feet at 30% relative humidity as about 5.5 dB. So, the total excess loss at 10 kHz would be very close to 11 dB over the distance from 2 feet to 200 feet. Adding this to 40 dB gives a total loss at 10 kHz of about 51 dB.
Nearfield and Farfield Considerations
If we make measurements too close to a sound source, we may not get the answers we would expect according to the discussion above. Typically, if we are closer to a source than about 5-times its greatest dimension, we are in its near field. Beyond that distance we are effectively in the far field. Note that there is no exact point where we leave one and go into the other; there is a transition range between the two.
Summing Levels in dB
Assume that a point source of sound has a level of 94 dB SPL at a given distance. Now, let us add another point source with the same 94 dB level, again at the same distance. What will be the resulting sum of the two? As both sounds are individually of the same level, their acoustical powers will be equal, and we will effectively be doubling that power when both are sounded together. This represents an increase of 3 dB, making a resultant level of 97 dB.
Let’s do another experiment. Assume that we have an existing sound pressure level of 94 dB; we want to add to it another sound pressure level that is only 84 dB. What will be the new level? This is a little more complicated, and we proceed in five steps as follows:
Let’s assign an arbitrary power to the first level (94 dB) of one watt. Since the second level (84 dB) is 10 dB lower, it has as power of 0.1 watt. Now, we add the two powers and come up with a sum of 1.1 watts.
Taking 10 log (1.1), we come up with an incremental level of 0.4 dB. Therefore, the resultant overall level is 94 + 0.4 = 94.4 dB SPL.
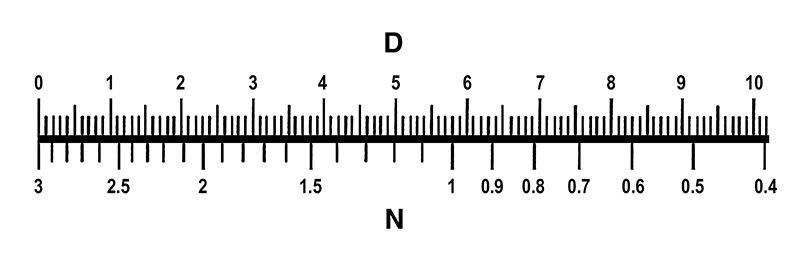
There is a simple way to arrive at this answer, and it is given by the nomograph shown in Fig. 1-20. Here, D is the difference in dB between the two levels. Read directly below D to obtain a number “N.” N is then added directly to the higher of the two original levels to arrive at the sum of the two.
Let’s rework the previous example using the nomograph. Taking the original 10 dB difference as D, we read the value of just slightly higher than 0.4 for the corresponding value of N. We then add that to 94 and get the answer of 94.4 dB.
Let’s rework the previous example using the nomograph. Taking the original 10-dB difference as D, we read the value of just slightly higher than 0.4 for the corresponding value of N. We then add that to 94 and get the answer of 94.4 dB.
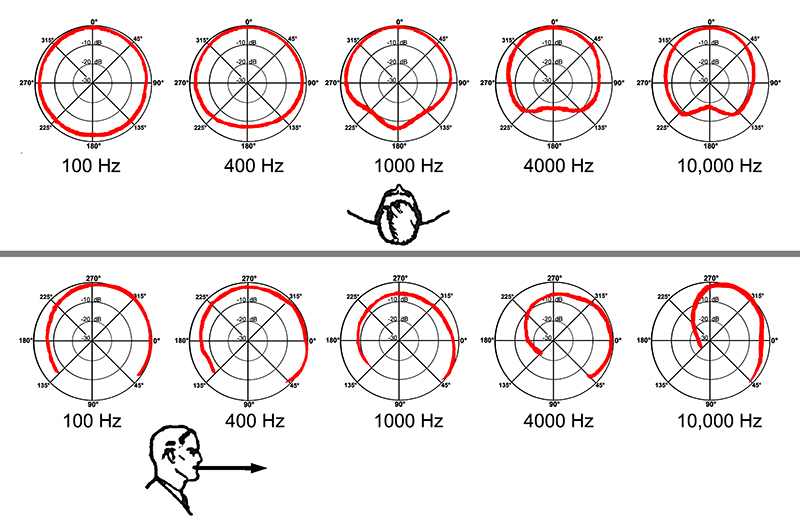
Directivity of Sound Sources
Many sound sources have radiation patterns that are directional. A trumpet, for example has directivity that is maximum along the axis of its bell, and a talker has directivity that is largely maximum in the forward direction. Loudspeakers that are used in sound reinforcement are likewise designed for maximum radiation within a clearly defined solid angle so that reinforced sound may be directed where it is needed. The basic presentation of directivity information is by way of the polar plot, in which the response of a device, under fixed signal excitation, is measured as it is rotated over a 360-degree angle in a single plane. An example of this is Fig. 1-21, which shows the polar response of the spoken voice in both vertical and horizontal planes. A separate polar plot must be made for each frequency or frequency band.
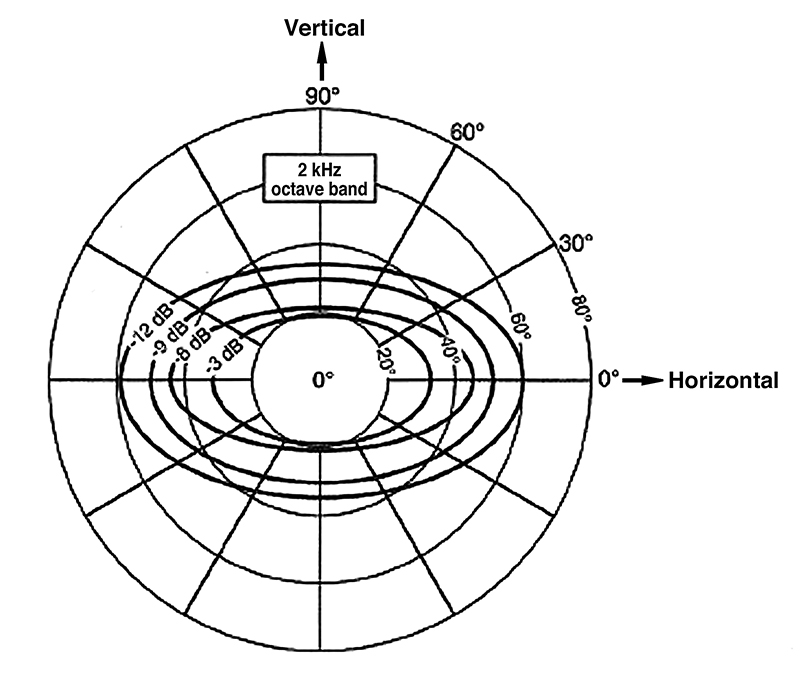
There are many methods for presenting directivity information, and some of them are shown in Fig. 1-22. Frontal isobars are shown at Fig. 1-22A; here, the -3, -6, -9 and -12 isobars are plotted in spherical coordinates as seen along the polar axis of a globe. A great deal of polar data must be measured in order to make such a detailed presentation as this.
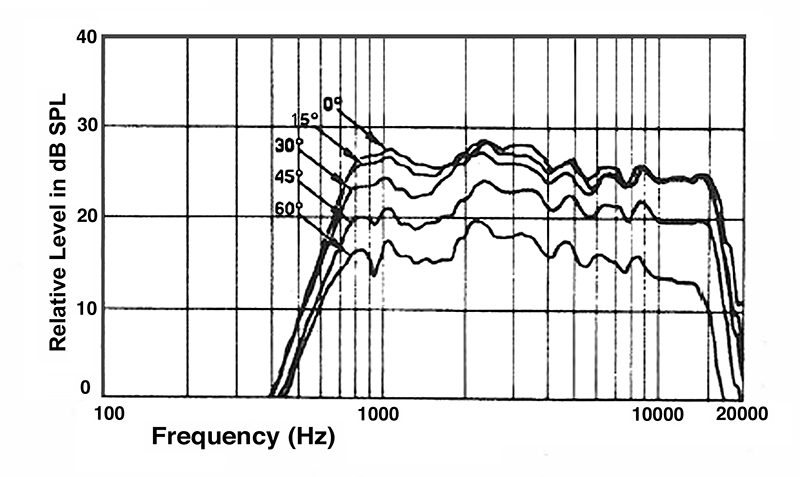
Off-axis frequency response curves, as shown at Fig. 1-22B, are useful in detailing the response of a loudspeaker over its normal frontal horizontal coverage zone.
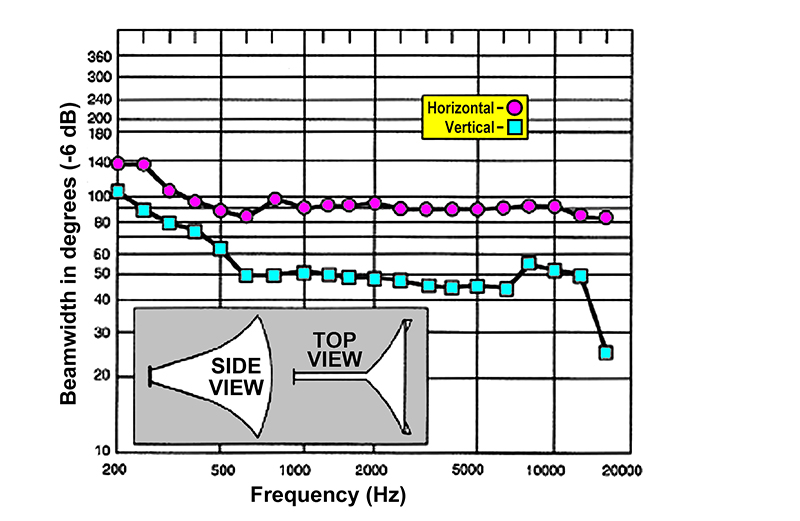
For many design applications, simple plots showing the angular spread between the -6 dB response angles in the horizontal and vertical planes are quite useful, as shown at Fig. 1-22C.
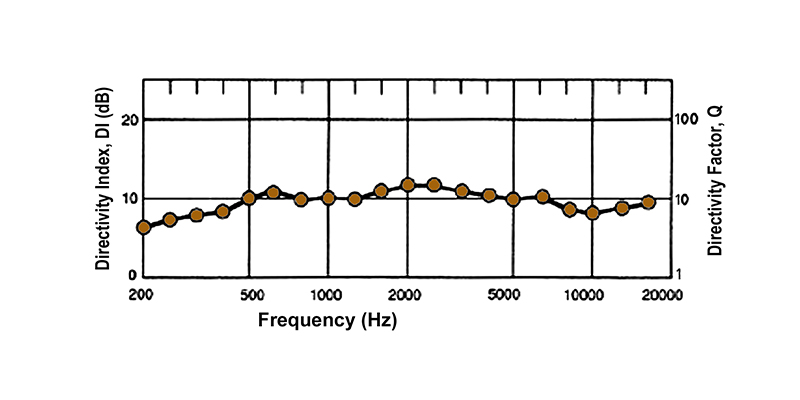
Finally, the plot of directivity index (DI) in dB is shown at Fig. 1-22D. DI is probably the most useful qualifier of directivity performance and involves only a single numerical value at each measurement frequency. DI is the ratio of sound level along a selected axis of a radiating device to the level that would exist at that measurement distance if the same acoustical power were radiated uniformly in all directions.
Directivity factor (Q) is another way of considering the same ratio. The relationship between DI and Q is given by:
DI = 10 log (Q) or Q = 10DI/10
The values of both Q and DI are used in audio engineering. Q represents a ratio, while DI is that same ratio expressed in dB.
More to Come
Next month, we’ll wrap up this discussion and explore: audio behavior in indoor soundfields, reverberant spaces, reverberation time and delve into room acoustics. Don’t miss it!
David K. Kennedy, a consultant on architectural acoustics and live-sound system design, has designed hundreds of sound systems for churches, schools, performing arts centers and AV contractors. Visit him at www.immersive-pa.com.



