It is widely known that different Digital Signal Processors (DSPs) sound different. I have heard this difference ascribed to everything from sample rate to the quality of the limiters, whatever that means. Certainly there is a difference to be found, but I suspect it is not going to be discovered using audiophile words like "warmth" and "depth." Largely to satisfy my own curiosity, I asked users of Sound Forums Network pro audio community (www.soundforums.net) to input a set of identical settings into whatever DSP they had access to and send me the results.
What I discovered is that there are large, easily measurable differences between one DSP and another in frequency response alone. As a result, one cannot take the setting from one processor and transfer them to another and expect the same results. This is why loudspeaker manufacturers provide settings for specific processors, and why when the wrong processor is used, sound quality is often compromised. Here we explain why, when using two different model DSPs, identical settings produce unequal results.
Bandwidth in Octaves Versus Q
The first part of this mystery has to do with two different and opposite definitions for filter bandwidth. Every loudspeaker requires equalization (EQ) to some extent, and for every EQ filter desired the DSP must be told the frequency, amplitude, and bandwidth of the filter (Figure 1)(See Endnote 1). Very wide bandwidth filters may be used to prop up the sagging low frequency response of a full range cabinet and very narrow filters used to cut out resonances in some horn-loaded compression drivers, for example.
There are two common definitions of filter bandwidth: Octaves, and Q. It is likely that you are familiar with octaves. A larger octave number means a wider filter. Most mixing console channel strip EQ is marked in octaves and we have all used 1/3 octave graphic equalizers. Circuit designers, on the other hand, are often more familiar with using Q (See Endnote 2) which is a measure of how under-damped a filter is. A larger Q number means a narrower filter. If that doesn't mean anything to you don't worry, I'm not a circuit designer either. The important thing to take away is that octaves and Q are reciprocals of each other.
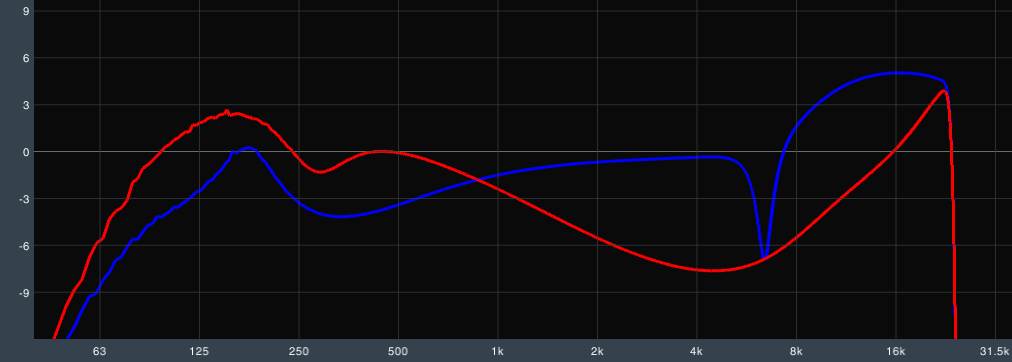
Step one in entering equalization into a DSP is therefore to determine whether the processor is expecting bandwidth or Q. Figure 2 demonstrates the consequences of entering Q into a device that uses bandwidth natively. The blue trace is how the filters are supposed to look. That narrow high frequency cut has a Q of 11.5, or a bandwidth of 1/8 octave. When entered incorrectly the processor attempts to create an 11.5 octave wide cut, which you can see in the red trace.
Fortunately it is possible to convert between the two standards. I have a handy reference available on my website (www.bennettprescott.com) that I often use to get "close enough." For more precise conversion there are a number of tools available on the Internet (See endnote 3) that may be found with a quick search. Once you have all your bandwidths in the right format, however, the real differences between DSP platforms become apparent.
Different Filter Definitions
Unfortunately for you, but perhaps fortunately for DSP manufacturers who want to lock users into their device "family," the challenges of copying settings between processors are not limited to bandwidth to Q conversion. Using Q when octaves bandwidth is required is a relatively simple error to avoid, with grossly audible and predictable results. Much less predictable is what happens when you take settings created on one DSP platform and enter them into another, expecting the same output.
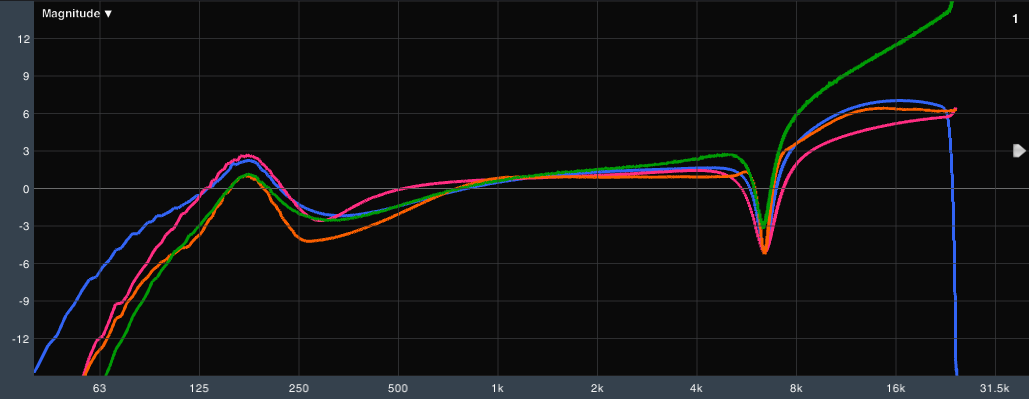
Figure 3 shows the frequency response of four different processors, each from a different manufacturer, using settings that I designed to showcase cross-platform differences. This is a cross-section of DSPs in terms of both price and popularity. As you can see, the differences can be considerable… several decibels error is commonplace, and in some areas the settings are off by as much as 9dB!
The problem is that manufacturers use different definitions for filter shape (See endnote 4). This is an issue that has always existed, but in the past you would rarely encounter someone painstakingly copying one analog mixer's channel EQ settings onto a different model mixer. In today's digital world the problem is exacerbated because transferring settings between devices is as simple as copying and pasting.
It's not that any of these four processors define their equalization filters wrong, per se. Deciding what shape a bell filter will have is like asking four people for driving directions: you might get four different answers, none of them wrong. What you see, therefore, is several filters with varying definitions of filter shape, which then interact with each other to create an even more varying final equalization curve. The reasons the filters are different could be that the digital filter shape was based upon an analog filter preferred in the past. It could be that the shape was mathematically convenient. Whatever the reason, when entering settings into one processor that were developed on another you might get lucky and be close, or you might as easily be off by a wide margin.
These differences in filter shape are not necessarily limited to products from different manufacturers. One of the largest system processor manufacturers once offered three products from the same product line, and none of them matched any other. Their current flagship processor does match one of their older processors, but not the one you might expect. One manufacturer also seems to use different filter math for every product it brands for other companies. Don't assume that because you believe two DSPs share hardware that their software will be identical.
It is possible to have the output of one processor accurately match another, but there is no simple conversion process that I am aware of. One must first measure the correct settings running on the correct processor using a program like Rational Acoustics Smaart. Then, while measuring the second processor, one can match its output to the stored measurement from the first, one filter at a time. This takes considerable effort and skill, and I can count on one finger the number of times I have done it. In almost any conceivable situation this is a waste of time. It makes far more sense to simply acquire the correct DSP with the correct settings.
Doing It Wrong
Since there is no standard for equalizer filter shape, the problems detailed above are largely understandable. Once a shape has been picked, it makes sense to stick with it so that your future products are compatible with your current ones. Since a lot of these filter shapes were decided upon at the dawn of commonly available DSPs, the lack of consensus is unsurprising. Even if a standard was created I doubt that many manufacturers would convert to it, as it would require new presets for every loudspeaker their gear is intended to process. That's not to say that all DSP math differences are forgivable, though.
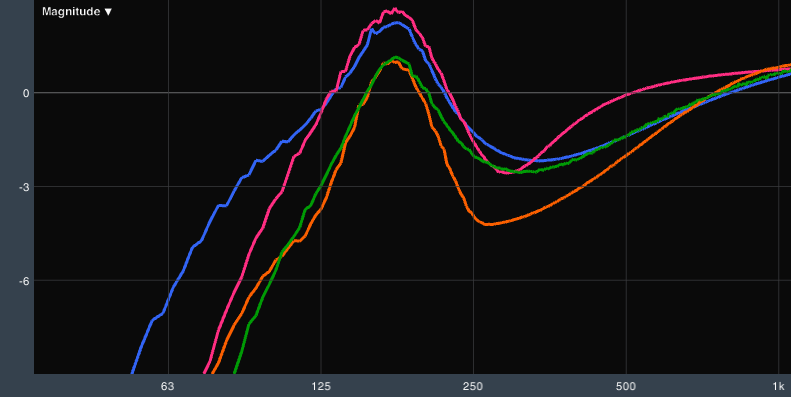
Some processors do it flat out wrong. One example is shown in Figure 4, a close-up of the high pass filter response of all four processors. Some of this behavior is confused by interaction with the low frequency boost EQ, but you can see that the blue trace deviates significantly from the other three. This is because it is the only one that is right! Three of these processors have defined the high pass filter at its -6dB point. That must have taken some effort since the math to do so isn't straightforward for this type of filter, which should be defined at its -3dB point. This change in definition moves the effective crossover point by about half an octave. That'll throw off your sub/mains crossover point for sure!
If even a name brand DSP cannot be relied on to correctly implement something as simple as a high pass filter, any assumption about the behavior of one processor relative to another must be thrown out the window. I deliberately chose a filter type that I knew suffered from rampant misdefinition, but one processor even changes the point at which the filter is defined depending on its slope. Good luck getting that to match any other DSP.
High Frequency Problems
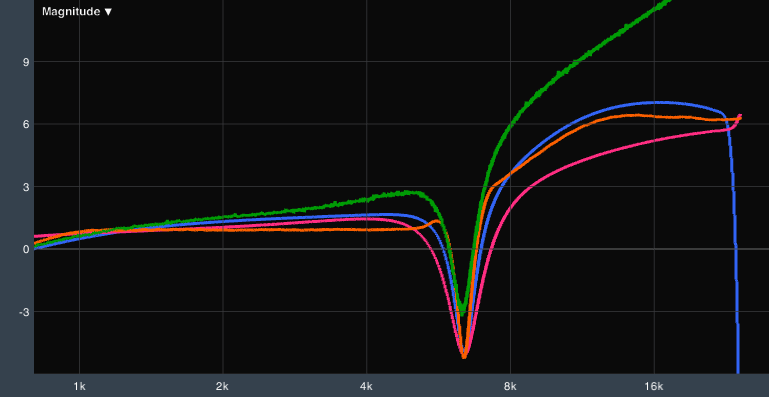
The final gotcha when moving settings between processor platforms is their handling of filter shape at frequencies close to the Nyquistpoint (half their native sample rate). Of the four processors shown in this article, two use 48kHz sampling and two use 96kHz sampling. A look at Figure 5 makes it clear which is which. The orange and blue traces change slope unpredictably, sagging and oscillating as they approach 24kHz. The other traces exhibit no such distortion. Whether they have similar problems at a higher frequency is unknown since all of these measurements were taken with a 48kHz sample rate. I do not mean to imply that higher sample rate devices are inherently better; a properly designed 48kHz device should not exhibit these problems and an improperly designed 96kHz device still will, although at frequencies beyond the limit of human hearing.
These distortions mean that not only might a device have a unique filter shape, but that filter shape might change with frequency. At least one processor I am aware of has EQ filters that get narrower as frequency climbs. Several have filters that become lopsided, narrower on the higher frequency side, as frequency rises above 10kHz. This behavior is even more unlikely to match that of other processors, further complicating the work of even a careful technician trying to match up loudspeaker presets using measurement software.
Passing Shots
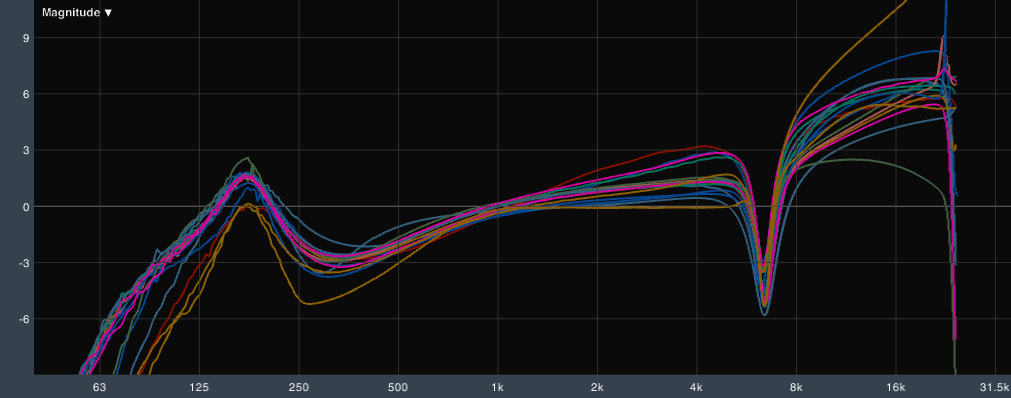
If this article has made anything clear, it should be that it is impossible to assume that settings from one processor will transfer correctly to another, even if the two processors are in the same product line from the same manufacturer. Figure 6 shows all of the name brand processor measurements I received for this article: the differences are not subtle. If you are lucky your settings might only be off by 3dB, which represents a serious tonal change. Unless you have taken the time to carefully match settings in your preferred DSP to a measurement of the proper settings in the recommended DSP, it is extremely unlikely that your loudspeaker will be processed correctly.
The consequence of using the wrong DSP, or the wrong settings, is often a poor impression of the connected loudspeaker. When different rental suppliers of the same loudspeaker each use different DSPs, the loudspeaker sounds different depending on who provided it. Several loudspeaker manufacturers have therefore been smart enough to force end users to buy into their complete system solution, including their amplifiers and their DSP. Every manufacturer of powered loudspeakers has done the same.
It is annoying to try to work with a loudspeaker that does not perform to expectations. It wastes time in troubleshooting, ruins the behavior of arrays, and makes you question yourself as an engineer. If in doubt, load a stock settings file for the loudspeaker into the DSP and see if the problems go away. Furthermore, make sure the DSP provided is one that the loudspeaker manufacturer supports: most only support one DSP. Modern loudspeakers require precise and complex processing to function as intended. Don't let a simple misconfiguration ruin your show.
Bennett Prescott is Director of North American Sales for ADRaudio, a European powered loudspeaker manufacturer. He lives in Connecticut, and can be reached at bennettprescott@gmail.com.
Special thanks go to Adam Robinson, Arthur Skudra, Chris Davis, Christian Tepfer, Dave Stiles, David Karol, Harry Brill Jr., Ivan Beaver, Jay Barracato, Jelmer de Jong, John Neil, and Klaus Zimmerman for providing the measurements I used to create this article.
[i] This Wikipedia article on Q can help you get a better handle on the specification: http://en.wikipedia.org/wiki/Q_factor
[ii] A precise octaves to Q conversion tool and formulas: http://www.sengpielaudio.com/calculator-bandwidth.htm
[iii] For more information see Rane Note 167 by Ray Miller: Why DSP Boxes Set the Same Way Differ. Available: http://www.rane.com/note167.html
[iv] The nature of the Nyquist frequency is gone over in great detail in this Wikipedia article: http://en.wikipedia.org/wiki/Nyquist_frequency



